Эта статья является частью книги «Измерьте свои экстрасенсорные способности». Больше читайте здесь.
Приложение 1
Таблица 1. Определение значимости для опыта распознавания цвета
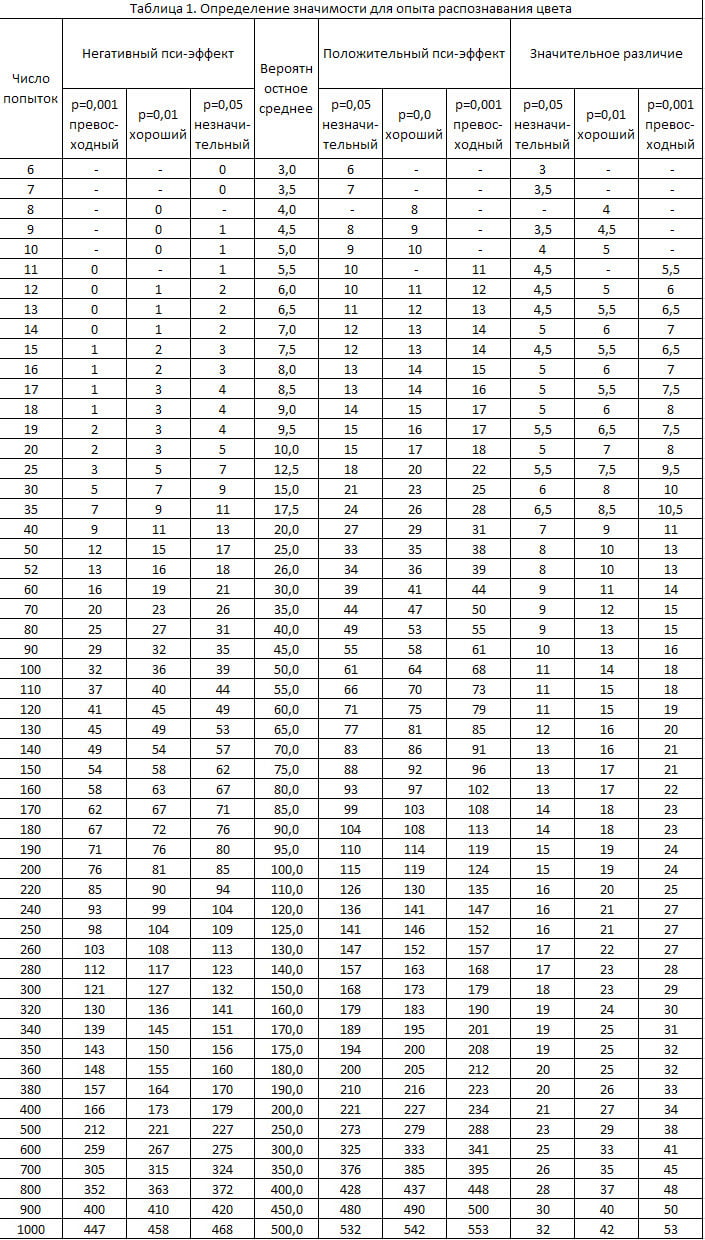
Таблица 2. Определение значимости для опыта распознавания масти
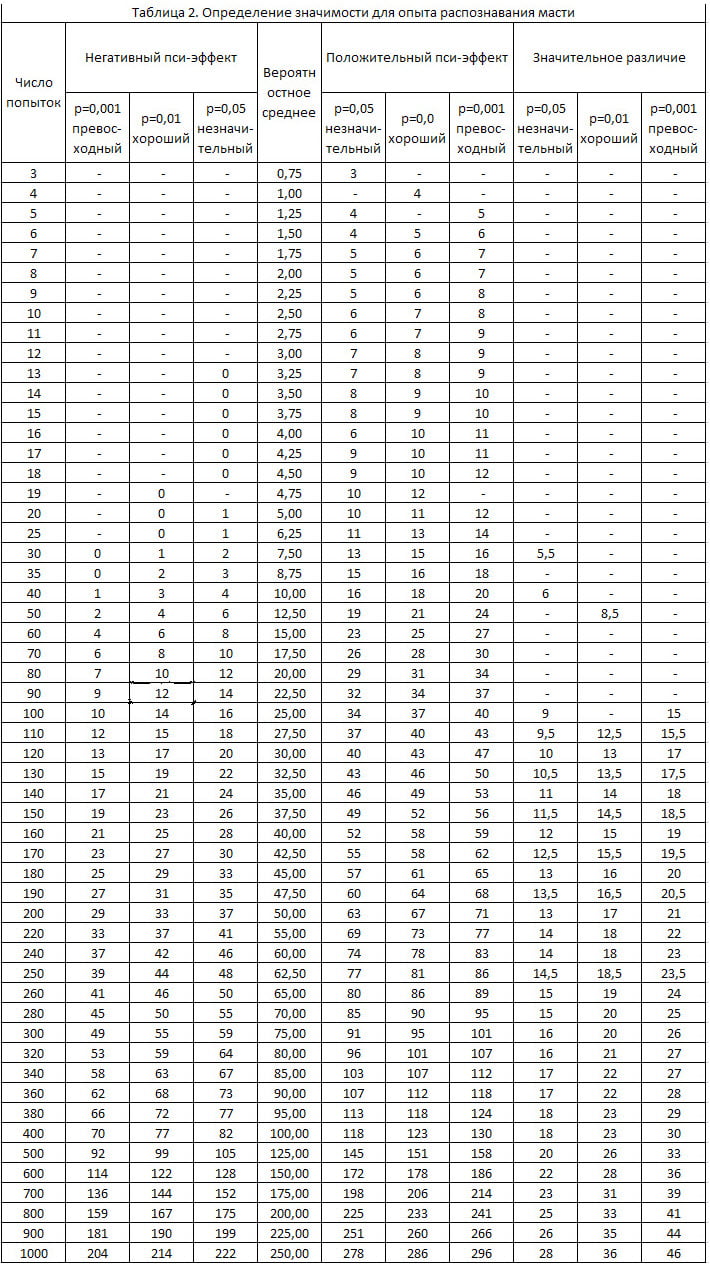
Таблица 3. Определение значимости для опыта распознавания цифр на картах (вероятность попадания 1/10)
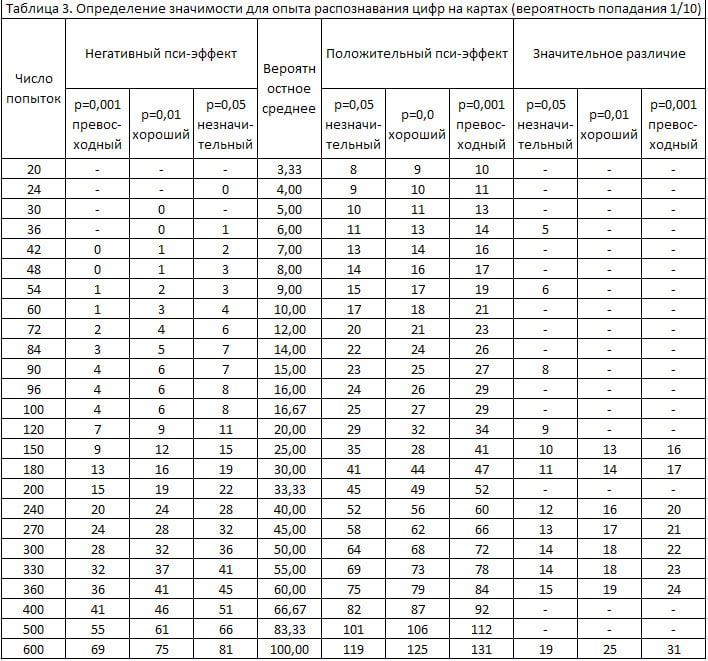
Таблица 4.
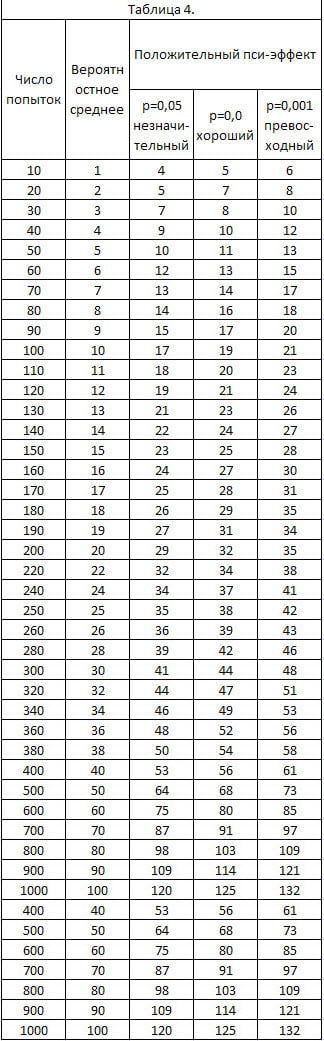
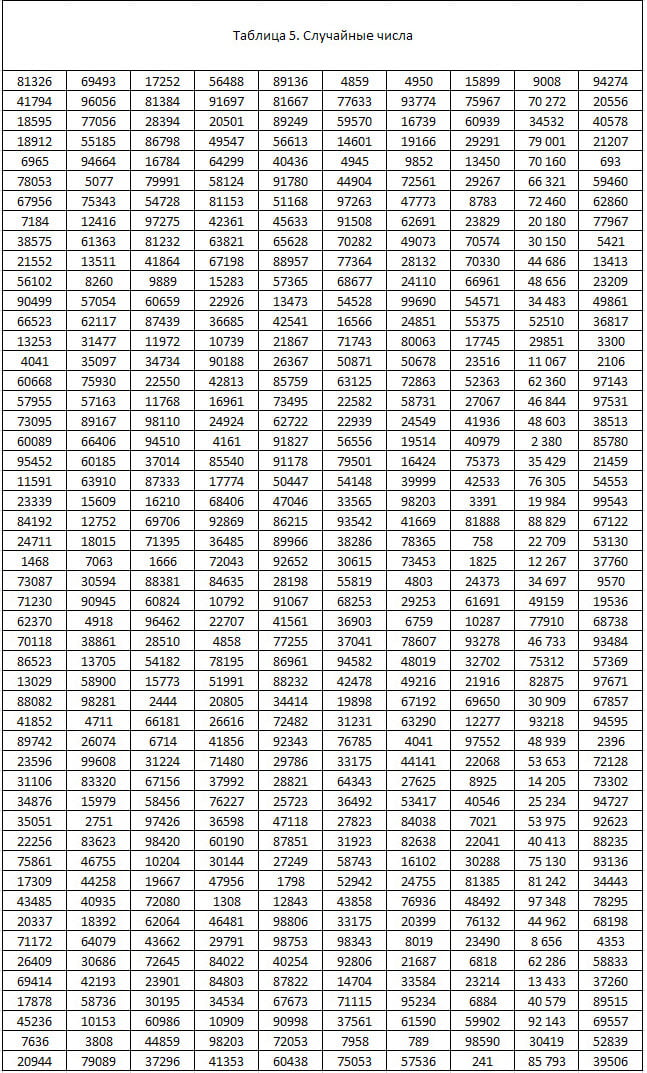
Таблица 5. Случайные числа
Числа в таблице содержат все цифры от 0 до 9 включительно и расположены в случайном порядке. Они могут быть достаточно легко преобразованы в другие типы при помощи следующих методов. Например, для выбора одной картинки из четырех (обозначенных 1,2,3, 4) вам нужны лишь эти четыре числа (выбор «один из четырех»). Приведенный ниже список показывает, как приспособить эту таблицу для выбора из различного числа равных возможностей.
Выбор из 2: 1, 3, 5, 7, 9 = 1; 2, 4, б, 8, 0 = 2.
Выбор из 3: 1, 4, 7 = 1; 2, б — 2; 3,7 = 3; 4, 8 = 4; 0 — пропустить.
Выбор из 4: 1, 5 = 1; 2, б = 2; 3, 7 = 3; 4, 8 = 4; 9, 0 — пропустить.
Выбор из 5: 1, 6 = 1; 2, 7 = 2; 3,8 = 3; 4, 9 = 4; 5, 0 = 5.
Выбор из б, 7, 8 или 9: просто пропускайте цифры вне выбранного диапазона.
Таблица содержит 2500 случайных чисел. На определенном этапе вам могут потребоваться дополнительные случайные числа, также вы можете обратиться к другой таблице случайных чисел (которую обычно можно найти в справочнике по статистике) или сгенерировать новую последовательность из этой таблицы, прочитывая данные по колонкам, а не по строкам. Можно также выбирать данные в обратном порядке или по диагонали.
Приложение 2
Z-критерий
Z-критерий может применяться для расчета вероятности случайного результата в пси-опыте с ограниченным выбором любого типа, использующего число попаданий и промахов. Этот критерий потребуется вам, если число попыток в вашем опыте отсутствует в таблицах 1-4.
Таким образом, результаты распознавания карт и бросания кубика могут обрабатываться при помощи Z-критерия, а результаты распознавания изображений с использованием ранговой суммы — нет.Z-критерий может использоваться при любом числе попыток и при любой вероятности попадания («один из двух», «один из трех», «один из четырех» и т.д.), если только число попыток не слишком мало.
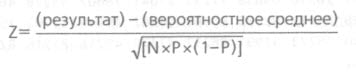
где N- число попыток, Р — вероятность случайного попадания в единичной попытке. Таким образом, при выборе «один из двух» р= 1 /2, или 0,5; если выбор «один из четырех», Р = 1 /4, или 0,25 и т.д. Вероятностное среднее рассчитывается очень легко, фактически, это произведение N х Р. Вам потребуется калькулятор, имеющий функцию квадратного корня, чтобы вычислить знаменатель формулы.
Какой смысл заложен в различных значениях Z-критерия? Хотя полное рассмотрение этого вопроса выходит за рамки данной книги, можно показать, что если Z больше или равно 1,96, то результат значим при Р = 0,05; если Z больше или равно 2,58, то результат значим при Р= 0,01; наконец, если Z больше или равно 3,30, то результат значим при Р = 0,001.
Еще два замечания относительно Z-критерия. Во-первых, Z-критерий не дает статистической достоверности, если знаменатель [N х Р х (1 -Р)] меньше 9. Вероятно, это означает, что число попыток мало и предпочтительно воспользоваться таблицами приложения 1.
Во-вторых, некоторые специалисты статистики дают следующую рекомендацию: если результат больше вероятностного среднего, то из числителя следует вычесть 0,5; если результат меньше ве-роятностного среднего, то к числителю следует прибавить 0,5. Это всегда уменьшает значение Z, таким образом, результат, по-лучавшийся значимым до внесения поправки, может оказаться незначимым. Эта поправка носит название «коррекция непре-рывности».
Ранговая сумма
В этом статистическом критерии используется сумма рангов «Целей» в опыте распознавания изображений (главы 5-7). Критерий можно применять для оценки значимости результата при любом числе попыток и при любом числе рангов (четыре картинки на выбор, как это сделано в данной книге, или больше, хотя число рангов во всех попытках должно быть равным).
Прежде чем давать формулу, два технических замечания. (В действительности этот критерий дает Z-значения и формирует Z-критерий, но во избежание путаницы мы назвали его ранговой суммой.) Во-первых, этот критерий не следует использовать, если число попыток менее 25; во-вторых, можно применять коррекцию непрерывности, хотя в приведенном ниже примере она не использована.

Таким образом, если R = 4, то R2 = 16.
Здесь также: если Z больше или равно 1,96, то результат значим при Р = 0,05; если Z больше или равно 2,58, то результат значим при Р = 0,01; наконец, если Z больше или равно 3,30, то результат значим при Р= 0,001.
Пример
Испытуемый героически выполнил 92 попытки распознавания изображений (выбор «один из четырех»). Ранговая сумма составила 209. Значимо ли отличается этот результат от вероятностного?
При выборе «один из четырех» средний вероятностный ранг в попытке будет 2,5; таким образом, вероятностная ранговая сумма в 92 попытках составит 922,5=230. Получен результат 209, отклонение от вероятностного — 21 (таким образом, результат лучше случайного).
Z=(209-230)/(92×15+12)= — 21 + 10,72= 1,96
Значение Zв точности равно значению Z-критерия при Р= 0,05. Заметьте, однако, что если использовать коррекцию непрерывности, то Z будет равно 1,91, т.е. не является значимым. Таким образом, результаты следует интерпретировать с осторожностью.





